配列変数

大量のデータを扱う場合の処理

4日目までの内容で、ほぼJava言語の基本的な概念が出てきました。しかし、これだけでは十分なプログラムができるわけではありません。実用的なプログラムを作るときに大事なことはたくさんありますが、特にここでは大量のデータを扱う場合について説明しましょう。C言語では、変数を用いて大量のデータを扱う場合、配列変数（はいれつへんすう）を用います。ここでは、配列変数の使い方を学ぶことにしましょう。

サンプルプログラム

配列変数について詳しく説明する前に、まずは以下のプログラムを入力・実行してみてください。

Sample501.java 
package day5;

public class Sample501 {

	public static void main(String[] args) {
		double one,two,three;
		double sum,avg; //  合計値、平均値を入れる変数
	    one = 1.2;
	    two = 3.7;
	    three = 4.1;    //  変数の代入
	    System.out.println(one + " " + two + " " + three);
	    sum = one + two + three;    //  合計値の計算
	    avg = sum / 3.0;            //  平均値の計算
	    System.out.println("合計値：" + sum);
	    System.out.println("平均値：" + avg);
	}
}
実行結果
1.2 3.7 4.1
合計値：9.0
平均値：3.0

このケースは、数値が3つだからよいですが、もしももっと増えたらどうなるでしょう？four,five,と、次々に定義する変数の数を増やしていかなくてはなりません。 しかし、このプログラムを、以下のように変更すると、大変楽になります。

Sample502.java 
package day5;

public class Sample502 {

	public static void main(String[] args) {
		 double[] d = new double[3];
		 double sum,avg; //  合計値、平均値を入れる変数
		 //  値を代入
		 d[0] = 1.2;
		 d[1] = 3.7;
		 d[2] = 4.1;
		 sum = 0.0;
		 for(int i = 0; i < d.length; i++){
			 System.out.print(d[i] + " ");
			 sum += d[i];
		}
		System.out.println();
		avg = sum / 3.0;
	    System.out.println("合計値：" + sum);
	    System.out.println("平均値：" + avg);
	}
}

実行結果は、Sample501.javaと一緒です。若干プログラムは長くなってしまいましたが、もしも変数が5個、10個、100個・・・と増えたときを考えてみてください。こちらのほうが、プログラムを変更する手間が少なそうです。

配列の大きさ

13行目に出てくる、d.lengthは、配列変数の成分の数を表します。この場合、dの成分は3つあるので、d.lengthは3となります。

配列の長さ
(配列変数名).length

これを用いることにより、配列変数の長さを取得することができます。

配列変数

では、一体、このプログラムはどのような仕組みになっているのでしょうか？6行目に出てくる、double d[] = new double[3];という記述が、配列変数（はいれつへんすう）の宣言です。配列変数とは、同一の名前で多数のデータを格納できる変数のことで、単に配列(はいれつ)とも呼ばれます。配列の諸式は以下のようになります。

配列の宣言
(変数の型名) (変数名)[] = new (変数の型名)[配列の数];
(変数の型名) [](変数名) = new (変数の型名)[配列の数];

したがって、この例で６行目は、double[] d = new double[3];と書くこともできます。

配列変数にも、変数名が存在します。この場合、dが変数名になります。[]の中に記述されているのが、配列の大きさで、この場合、サイズは3になります。

添字

この処理により、d[0]、d[1]、d[2]という3つのdouble型の変数が使用可能になります（図5-1）。9行目から11行目の間で、これらの変数に値を代入しています。なお、ここで[]の中に書いてある数字を、添字（そえじ）と言います。例えば、「d[1] = 3.7;」という処理は、この配列の2番目の変数に、3.7という値を代入することを意味します（図5-2）。この数値は必ず0から始まりますので、配列の大きさが3の場合は、2までになります。

図5-1.配列の宣言図5-2.配列変数への値の代入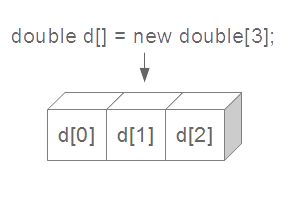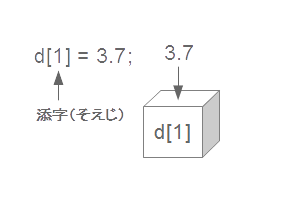
Javaの配列の宣言Javaの配列変数への代入

添字が、配列の範囲を超えていてもエラーにはなりませんが、実行時に異常終了したりすることがありますので、気をつけましょう。

配列変数を使うメリットは、実はこの添字が使えることにあります。13行目から16行目のforループの中で、添字に整数型変数iを用いています。これにより、プログラムを変更して、配列の大きさを変化させても、for文に条件式の値を変化させるだけで対応できます。

配列の初期化

ところで、配列変数の宣言と初期化ですが、もう少し、楽にならないものなのでしょうか？実は、以下のようにすると、配列変数の宣言と初期化を一度に行うことができます。

Sample503.java 
package day5;

public class Sample503 {

	public static void main(String[] args) {
	    int n[] = { 5,4,3,2,1 };
	    String s[] = {"ABC","DEF","GHI" };
	    int i;
	    //	整数型配列変数nの成分表示
	    for(i = 0; i < n.length; i++){
	        System.out.print(n[i]+" ");
	    }
	    System.out.println();
	    //	文字列型配列変数nの成分表示
	    for(i = 0; i < s.length; i++){
	        System.out.print(s[i]+" ");
	    }
	    System.out.println();
	}
}
実行結果
5 4 3 2 1
ABC DEF GHI

実行結果を見るとわかるように、6～7行目で行っている処理は、配列のを生成し、同時に値を代入しています。例えば、nについては、以下のような処理を行っています。

配列の宣言と初期化
int n[] = { 5,4,3,2,1 };
    ↓ この処理は、以下の処理に相当
int n[] = new int[5];
n[0] = 5;
n[1] = 4;
n[2] = 3;
n[3] = 2;
n[4] = 1;

文字列変数sについても同様で、3個の成分を作り、s[0]からs[2]に値を「ABC」「DEF」「GHI」にしています。

多次元配列

サンプルプログラム

最後に、配列変数の応用である、多次元配列（たじげんはいれつ）について説明しましょう。多次元配列とは、複数の添字をつけることができる配列変数です。そのなかで、最も基本となる二次元配列の例をここでは紹介します。以下のプログラムを実行してみてください。

Sample504.java 
package day5;

public class Sample504 {

	public static void main(String[] args) {
		int a[][] = new int[3][4];
	    int m,n;
	    //  二次元配列に値を代入
	    for(m = 0; m < a.length; m++){
	        for(n = 0; n < a[m].length; n++){
	            a[m][n] = m+n;
	        }
	    }
	    //  成分の表示
	    for(m = 0; m < a.length; m++){
	        for(n = 0; n < a[m].length; n++){
	            System.out.print(a[m][n]+" ");
	        }
	        System.out.println();
	    }

	}
}
実行結果
0 1 2 3
1 2 3 4
2 3 4 5

二次元配列

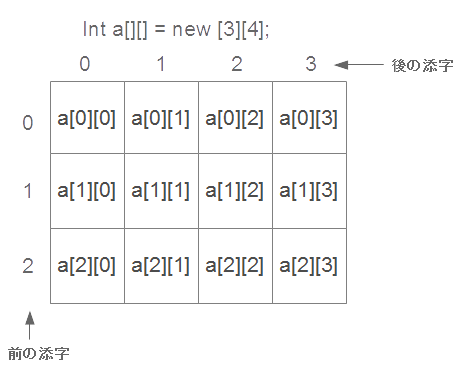
二次元配列aには、2つの添え字をつけることができます。これにより、二次元の配列を作ることが可能です。（図5-3）

図5-3.二次元配列のイメージ
二次元配列のイメージ

配列の大きさは、a.lengthが、3、a[m].lengthが4になります。これは、newの後の[]内に記した配列の成分数の通りです。

二次元配列の理由範囲は非常に高く、さまざまな表や、座標などのデータを表すものとして使用されます。わかりやすい例でいくと、表計算のような処理は、二次元配列を用いれば、非常に簡単に実現できます。

理論的には、このようにして添字を増やすことにより、二次元、三次元・・・といった多次元の配列変数を作ることは可能です。しかし、実際用いられる多次元配列は、ほとんどがこの二次元配列です。

不揃いな二次元配列

サンプルプログラム

Sample504.javaでは、長方形の形になる二次元配列でしたが、この配列の構造は、不揃いにすることができます。以下のサンプルを実行してみてください。

Sample505.java 
package day5;

public class Sample505 {

	public static void main(String[] args) {
		int a[][] = { {0,1},{2},{3,4,5,6}};
	    //  成分の表示
	    for(int m = 0; m < a.length; m++){
	        for(int n = 0; n < a[m].length; n++){
	            System.out.print(a[m][n]+" ");
	        }
	        System.out.println();
	    }
	}

}
実行結果
0 1
2
3 4 5 6

このように、縦、横の成分がばらばらになるようなケースもあります。図にすると、以下のようなイメージになります。（図5-4.）

図5-4.不揃いな配列のイメージ
二次元配列のイメージ

練習問題 : 問題5.